GRADO SÉPTIMO
PRIMER PERIODO
GUIA # 1
Identificar diferentes usos de los números Naturales
Reconocer las características
de los números Naturales Y decimales
DIVISOR: Como ya se vio, un múltiplo es un número se obtiene de multiplicar cierto número por otro natural; ahora bien, un divisor es un número que divide exactamente a otro número.
Para determinar si un número es divisor de otro, se aplican los criterios de divisibilidad, que fueron objeto de estudio en la G.A. sesión 2.30 del año anterior.
Ahora, para hallar todos los divisores de un cierto número se buscan las parejas de números o factores que al multiplicarse den como resultado ese número; para ello, se aplica el método de ensayo y error. Esto indica que se deben ir multiplicando factores de manera que se obtenga el número buscado. Para esto, se debe tener en cuenta que un número tiene una cantidad limitada de divisores.
CRITERIOS DE DIVISIBILIDAD ENTRE 2, 3, 5,6 y 7
Los videos, si los observas con atención y tomas nota te ayudaran mucho
https://www.youtube.com/watch?v=SkwBerst0zM
https://www.youtube.com/watch?v=TIjkDkBLH8c
CRITERIO DE DIVISIBILIDAD ENTRE 2
Un número es divisible por 2 si el dígito de las unidades es 0, 2, 4, 6, 8.
EJEMPLO:
4520 628 724 436
Observe: 4520 termina en cero por lo tanto es divisible por 2
Los demás números terminan en número par, por lo tanto son divisibles por 2
CRITERIO DE DIVISIBILIDAD ENTRE 3
Un número es divisible entre 3, si la suma de sus dígitos es un múltiplo de 3.
EJEMPLO:
423 sumamos 4+2+3=9, es divisible entre 3, porque 9 que es el resultado es múltiplo de 3
1623 sumamos 1+6+2+3 =12, es divisible entre 3, porque 12 es múltiplo de 3
CRITERIO DE DIVISIBILIDAD ENTRE 5
Un número es divisible entre 5 si la cifra de las unidades simples es cero o cinco.
EJEMPLO:
425 700 675 120
CRITERIO DE DIVISIBILIDAD ENTRE 6
Un número es divisible por 6 si es par y múltiplo de 3 simultáneamente
La diferencia es 0, por lo
tanto, 84 es divisible entre 7.
245: se duplican las unidades: (5
× 2 = 10); se resta el resultado a las cifras restantes:
24 – 10 = 14
El resultado es 14, número que se identifica rápidamente como múltiplo de 7, por lo tanto,el número 245 es divisible entre 7.
CRITERIO DE DIVISIBILIDAD ENTRE 10
Un número es divisible por 10 si termina en cero.
Una de las ideas relacionadas con la operación de
multiplicar números naturales es la de mínimo común múltiplo de varios números.
Dicha idea está en la base de muchos problemas de la economía, la ciencia y la
tecnología, en los que se busca encontrar un mínimo de diversas
cantidades. Cuando se ordenan de menor a
mayor los múltiplos de dos o más números, se observa que algunos se repiten. A
estos números que se repiten y que son comunes a los números dados, se les
llama múltiplos comunes.
EJEMPLO:
Observe los primeros múltiplos de los números 4, 6
y 8.
Múltiplos de 4: [ 0, 4, 8, 12, 16, 20, (24), 28, 32, 36, 40, 44, 48, 52... ]
Múltiplos de 6: [ 0, 6, 12, 18, (24), 30, 36, 42, 48,
54, 60, 66... ]
Múltiplos de 8: [ 0, 8, 16, (24), 32, 40, 48, 56, 64,
72, 80, 88... ]
Aplicando lo anterior podemos decir que, el mínimo común múltiplo de los números
4, 6 y 8 es el 24. ya que es el que se repite (común) en los tres conjuntos de números.
Esta expresión se simboliza así: mcm (4, 6, 8) = 24
El mínimo común múltiplo de dos o más números es el menor de los múltiplos comunes a dichos números, que sea diferente de cero.
Un procedimiento sencillo para obtener el mcm de varios números es el de la factorización simultánea, el cual se detalla a continuación:
EJEMPLO: halla el mínimo común múltiplo de 4, 6 y 8.
Aplicando los criterios de divisibilidad y factorizando en forma simultánea los números
4, 6 y 8,
se tiene que el primer factor primo es 2, al efectuar mentalmente las
divisiones:
Aplicando el mismo criterio de divisibilidad, se ve que el 3 no es par, por lo tanto, se reescribe en el siguiente renglón, junto con los cocientes de los otros números a ser divididos:
Se aplica
otra vez el criterio de divisibilidad entre dos, pero obsérvese que nuevamente
el 3 no es par, por lo tanto, se reescribe en el renglón de abajo, además de
los cocientes respectivos:
Se aplica
el criterio de divisibilidad para el último número que queda, 3, y se efectúa
la división, anotando en el siguiente renglón el cociente obtenido:
Su factorización termina cuando
la unidad queda como residuo al final de la columna de cada numero factorizado.
Finalmente, la representación será: mcm (4, 6, 8) = 24
El siguiente video en su primera parte, te mostrara otra forma para hallar el m.c.m
MÁXIMO COMÚN DIVISOR ( M.C.D)
En matemáticas, se denomina máximo común divisor o MCD al mayor número que divide exactamente a dos o más números a la vez.
EJEMPLO:
Si se buscan los divisores de dos o más números, se
observa que uno o varios coinciden en todos ellos. Esos divisores comunes son
de gran ayuda en la resolución de problemas cotidianos.
Divisores
de $15 000 son [ 50, 100, 200, 500, 1 000 ]
Divisores
de $20 000 son [ 50, 100, 200, 500, 1 000 ]
Se observa que el mayor de los divisores comunes (pensando en las denominaciones de billetes) es 1000. El mayor valor de los billetes es 1 000.
El Máximo común divisor (MCD) de dos o más
números es el número mayor que los divide a todos exactamente.
Entonces M:C:D( 15.000 y 20.000) = 1000
En
matemáticas existen procedimientos que nos permiten resolver problemas de
manera
directa y sencilla. A continuación se presenta un
procedimiento fácil para obtener el MCD.
debía
empacarlas de tal manera que en cada paquete hubiese igual número de
calculadoras
del mismo
color.
Obsérvese
que los números 4, 6 y 7 no tienen
divisor común, con excepción del uno. Por lo tanto, se detiene el proceso y
puede manifestarse que el MCD de los números
16, 24 y 28 es el producto de los
divisores comunes.
Por lo
tanto:
MCD (16, 24, 28) = 2 x 2
El 4 indica el máximo número de paquetes que se pueden
formar, de tal manera que cada paquete contenga el mismo número de calculadoras
del mismo color.
En el video encontraras, explicación sobre una forma de hallar M.C.D, Aprovechalo!
FACTORIZACIÓN
En algunos cálculos matemáticos se hace necesario
hallar los factores de un número; este
proceso se conoce como descomposición en factores o
simplemente factorización de ese
número.
Ejemplo:
4 = 4 x1 =
2 x 2 x 1
8 = 4 x 2 = 2 x 2 x 2 x 1
12 = 2 x 6 = 2 x 2 x 3 x 1
Se escribe el
número que se quiere factorizar y a su derecha se traza una línea vertical. 40
Se aplican los criterios de divisibilidad, efectuando las divisiones entre
primos sucesivos en orden creciente,esto es,de menor a mayor.Los cocientes se
van
Escribiendo
en columnas debajo del primer dividendo.
(a) 52 y 72 (b) 82 y
90 (c) 114 y 92
b. Tres buses salen el mismo día de la terminal de transporte del Norte de la ciudad de Medellín. El primero regresa cada seis días, el segundo cada cinco y el tercero cada tres. ¿Cuántos días pasarán para encontrarse todos nuevamente?
NÚMEROS PRIMOS Y COMPUESTOS
En ocasiones, al determinar los factores o divisores de uno o más números dados, se observa que algunos tienen varios divisores, otro tiene sólo uno y los demás, curiosamente, tienen únicamente dos factores tal como lo observaste en el tema de los divisores de un numero natural.
A los números que tienen dos divisores (el número 1 y a sí mismos) se les conoce como números primos.
A los números
que tienen más de dos divisores se les conoce como números compuestos. Por lo que respecta al número 1, se dice que
no es número primo ni tampoco número compuesto, ya que tiene únicamente un
divisor.
Ejemplo de números primos
83: el conjunto de sus divisores es {1,83}
43: el conjunto de sus divisores es {1,43}
Ejemplo de números compuestos
8: el conjunto de sus divisores es {1, 2, 4, 8}
20: el conjunto de sus
divisores es {1, 2, 4, 5, 10 y 20}
POTENCIACION, RADICACION Y LOGARITMACION
La potenciación es una operación que facilita la resolución de diversos problemas. Ejemplo: Una caja contiene 20 paquetes de cerillas, cada paquete contiene 20 cajitas y, cada una de éstas tiene 20 cerillas, ¿cuántas cerillas tiene en total la caja? Para resolver este problema se hace necesario la siguiente multiplicación. 20 paquetes × 20 cajitas × 20 cerillas = 8 000 Una forma simplificada de expresar esta operación es también: 203 = 8 000 Por lo tanto, la potenciación, como un caso particular de multiplicación, es la operación que transforma a dos números –uno que se repite como factor y otro que indica las veces que el primero se ha de repetir– en una potencia. Así, una multiplicación de factores iguales se puede expresar mediante una potencia:
3 × 3 × 3 × 3 × 3 × 3 = 36 = 729
lo que significa tomar 6 veces el mismo factor El número que se multiplica por sí mismo recibe el nombre de base. En este caso, 3 es la base. Las veces que la base se toma como factor se indica con un pequeño número escrito en la parte superior derecha, al que se conoce con el nombre de exponente; en este ejemplo, corresponde al número 6. El número 729 es la potencia, producto de la multiplicación de los factores iguales según el exponente
36 EXPONENTE = 729 potencia
Base
Otros ejemplos son:
54=
5 × 5 × 5 × 5 = 625
26
= 2 × 2 × 2 × 2 × 2 × 2 = 64
92
= 9 × 9 = 81
En este último ejemplo, el exponente 2 se lee cuadrado o segunda potencia, y si fuera 93 se leería cubo o tercera potencia. Del 4 en adelante, se dice: cuarta, quinta, sexta potencia,...
Hallar la raíz cuadrada de un número es la operación inversa a encontrar la segunda potencia, y consiste en hallar un número que multiplicado por sí mismo sea igual al radicando o se aproxime a él. Así:
√ 81 = 9 porque 9 × 9 = 81
Para el Logaritmo se tiene:
Log9 de 81 = 2 Observemos que acá debemos de encontrar el exponente.
La siguiente tabla te muestra la interconversión de operaciones, te ayudará en la actividad
ACTIVIDAD #3
RESOLVER:
a. El cubo del número natural 4 es
b. El cuadrado del número natural 9 es:
c. La raíz cubica del número natural 64 es :
d. La potencia de 44 es :
e. La raíz QUINTA de 32 es :
f. La potencia de 82 es :
g. La raíz cubica de 125 es
h. Log 3 de 81 es :
JERARQUÍA DE OPERACIONES
La jerarquía de
operaciones es un método para resolver operaciones con
múltiples operadores; saber realizarla te servirá para resolver los diversos
problemas que se presenten en tu vida cotidiana
Primero se deben
ejecutar las operaciones agrupadas en paréntesis, luego las
potencias y raíces, en tercer lugar las multiplicaciones y divisiones en orden
de aparición, y finalmente las sumas y restas en orden de aparición.
Para
evitar confusiones y errores se ha convenido en que cuando no hay paréntesis,
dado que los signos + y – separan cantidades, se efectúan las operaciones en el
siguiente orden de izquierda a derecha
- Potencias y raíces
- Multiplicaciones y
Divisiones
- Adiciones y
Sustracciones
ACTIVIDAD #4
Aplica la jerarquia de operaciones
a) 18 + 16 ÷ 2 –
5 . 2 – 18 =
b) 63 –7 + 7 – 14 =
c) 30 – (26 + 15 + 14) =
d) 32/4 + 70 – 17 –1 2 =
e) a) 4. √4 + 32 / 3 + 4 + 6 =
f) 23 +10 / 2 +5 ·3 +4 −5 ·2−8 +4 22−18 / 3 =
¿QUE DEBES ENVIAR?
Como te darás cuenta, a lo largo de la guia hay 4 actividades, en ese mismo orden
las debes resolver y enviarlas al correo de los docentes respectivos.
No olvides ser muy ordenado en la solución de las actividades
OVIDIO PUERTA: 7.1 - 7.2 - 7.3 Y 7.4
ovipuerta@hernanvillabaena.edu.co
DUDAS: Whatsapp 3126812851
CONSUELO TABORDA: 7.5
ctaborda@hernanvillabaena.edu.co
DUDAS :WHATSAPP 3128364393
Esta guía tendrá 3 notas
NOTA 1: ORGANIZACIÓN Y PUNTUALIDAD EN LA ENTREGA DE LA GUIA
NOTA 2: RAZONAMIENTO MATEMÁTICO EN LA SOLUCIÓN DE ACTIVIDADES
NOTA 3: CLARIDAD DE CONCEPTOS PARA LAS DIFERENTES SOLUCIONES
FECHA DE ENTREGA: Tienen plazo hasta el lunes 15 de febrero a las 12:00 del mediodía, pero pueden enviarla antes si la terminan
GUIA # 2
MARZO 1/2021
NÚMEROS DECIMALES Y DIAGRAMA DE BARRAS
|
OBJETIVO: comprender afianzar los conocimientos sobre las operaciones con números decimales Interpretar
datos representados en tablas y sacar conclusiones estadísticas. |
Observe que la parte entera está antes de la coma o del punto y que puede ser un número cualquiera o puede ser cero. La parte decimal va después de la coma.
Se lee la parte entera, indicando los enteros que son y a continuación la cantidad de decimales
indicando el orden de la última cifra decimal
27.2 ------- 27 enteros y 2 décimas
- 0, 325 ----------- 0 enteros
y 325 milésimas
TRANSFORMACIÓN ENTRE DECIMALES Y FRACCIONES
a. Convertir #decimal a fracción( recuerde criterios de divisibilidad)
Ejemplo:
Convertir 0.75 en una fracción
Se coloca el numero decimal sin la coma como numerador y
el denominador será el uno seguido de tantos ceros como cifras decimales tenga
el número y luego simplificamos
75 = 15 =
3 ( dividimos entre 5 , porque los dos números
terminan en cero y cinco)
100 25 5
b. Convertir fracciones decimales a
#decimales
Ejemplo: convertir 135/10 a número decimal
Escribimos el numerador y se corren a la izquierda del numerador tantos
lugares como ceros hayan en el denominador y se coloca la coma
135 es el numerador y como el denominador solo tiene un cero, corremos
un lugar a la izquierda y la coma allí
Y nos quedaría : 13,5
Operaciones con números decimales
Suma y resta
Para sumar y restar
números decimales, debemos anotar cada valor en forma vertical, para facilitar
la operación, de tal manera que la coma quede en la misma columna, incluso si
la parte entera de un valor tenga más cifras que el otro, como se ve en el
ejemplo siguiente:
3,48 + 9,657
colocamos las cantidades en forma vertical y que la coma quede en la
misma columna
3,48
dos cifras decimales
9,657
tres cifras decimales
A continuación, se iguala el número de cifras decimales de cada valor si es necesario, añadiendo uno o varios ceros al valor con menos cifras decimales para que queden con el mismo número, pues el cero añadido a la derecha de la parte decimal no altera el valor, así:
3,480
9,657
Finalmente se suma de manera tradicional, sin tomar
en cuenta la coma, y al resultado final se le añade la coma en la misma
posición que se encuentra en ambos valores sumados o restados.
3,480+
9,657
13,137
Para la resta se procede igual, solo se debe tener
en cuenta que el minuendo es la cantidad mayor
Ejemplo : restar
8,47 - 12,120
minuendo:12,120 sustraendo 8,47
Se colocan en forma vertical y se igualan las
cifras decimales con ceros
12,120 –
8,470
3,650
observe que la coma, queda en la misma columna
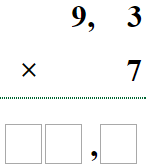
Multiplicación
Para multiplicar dos números decimales, o un número decimal por un número entero, se resuelve la operación sin tomar en cuenta la coma. Luego el número de cifras decimales será la suma del número de cifras decimales de los dos factores, es decir que, si un factor tiene dos cifras decimales y el otro tiene una cifra decimal, quiere decir que el resultado deberá tener tres cifras decimales, como en el siguiente ejemplo
multiplicar: 3,25 x 2,7
3,25
-- hay 2 cifras decimales
x 2,7 -- hay 1 cifra decimal
2275
650
8,775 ___ el resultado tendrá 3 cifras decimales que se empiezan a contar de derecha a
izquierda y allí se coloca la coma
Para multiplicar números decimales por cifras que son múltiplos de diez,
solo recorremos la coma hacia la derecha tantos espacios como ceros tenga el
múltiplo de diez, y en el caso de que tengamos que seguir recorriendo y ya no
haya cifras decimales, añadimos ceros al resultado, de esta manera:
3,568×10 = 35,68
3,568×100 = 356,8
3,568×1000 = 3568
3,568×10000 = 35680
Tenga presente este concepto para la división
División: La
opción más sencilla para dividir decimales es colocarlos como una fracción y multiplicar
numerador y denominador por múltiplos de 10( amplificación), los cuales
corresponden al mayor número de decimales que tenga la fracción, esto se hace
para transformar el decimal en entero
Ejemplo : 24,56 ÷4,2
Colocamos los dos números como una fracción
24,56
4,2
igualamos cifras decimales con ceros
24,56 x 100 = 2456
4,20 420
multiplicamos por 100, porque cada número
tiene 2 cifras decimales
recuerde que para multiplicar corre tantos
lugares a la derecha, como
ceros tenga el múltiplo de 10
Luego se hace la división normal :
Potenciación: En la potenciación
de números decimales existe un método rápido y sencillo que puede ayudar en su
comprensión y en la solución de ejercicios.
Se tiene un numero decimal elevado a una potencia, siempre miramos la
última cifra decimal, en caso que el numero entero sea cero y elevamos esta
cifra según indique el exponente
Ejemplo: ( 0,03)2
el ultimo decimal es 3 y el exponente es 2
Elevamos al cuadrado el numero 3
(0,03)2 =
9
Para completar el resultado miramos las cifras decimales y las
multiplicamos por el exponente
Hay 2 cifras decimales y el exponente es 2 entonces 2x2=4
Quiere decir que nuestro resultado tendrá 4 cifras decimales ( no cuatro
ceros)
(0,03)2 = 0 ,0009 cuatro
cifras decimales, después de la última cifra colocamos la coma y el cero
Entonces (0,03)2 = 0
,0009
Si el numero entero es diferente de cero:
(2,4)2 acá el numero
entero es 2
En este caso , imaginamos que no existe la coma y elevamos todo el
numero al exponente indicado, en este caso lo elevamos al cuadrado
( 24)2 = 576 para hallar el numero decimal, reescribimos
con la coma
(2,4)2 = 576 miramos el número de cifras decimales y lo
multiplicamos por el exponente
Hay una
cifra decimal y el exponente es 2 ,
entonces 1x2=2
Quiere
decir que el resultado tiene 2 cifras decimales, colocamos la coma
Quedaría: (2,4)2 = 5,76
RADICACIÓN: Para la radicación hacemos lo siguiente: miramos el último
número que hay debajo del radical , y sacamos la raíz que indique el índice
si no tiene índice es una raíz cuadrada y el índice es 2
Vemos que el último número debajo del radical es 9, sacamos la raíz
cuadrada de 9
Ahora dividimos el número de cifras decimales entre el índice
Hay 4 cifras decimales y el índice
es 2 entonces 4/2 =2
Quiere decir que el resultado tiene 2 cifras decimales
Observe cuando el numero entero es diferente de cero
Estadística:
DIAGRAMA DE BARRAS( GRÁFICO DE BARRAS)
Un gráfico de barras o gráfico de
columnas, es una forma de representar gráficamente un conjunto de datos o
valores mediante barras rectangulares de longitud proporcional a los valores representados. Los gráficos
de barras pueden ser usados para comparar cantidades de una variable en
diferentes momentos.
TENGA EN CUENTA EN EL MOMENTO DE
REALIZAR EL GRÁFICO
·
El ancho
de la barra debe ser uniforme para todas las barras del diagrama.
·
La longitud
de la barra debe ser proporcional a la cantidad que representa.
·
El
espacio de separación entre barras por cada categoría debe ser constante.
·
Las
barras en estos gráficos pueden disponerse vertical u horizontalmente.
Es importante saber, que los datos correspondientes a una variable los podemos colocar en una tabla de datos y que luego miramos cuantas veces se repite cada dato, las veces que se repite un dato se llama frecuencia ABSOLUTA, la frecuencia RELATIVA se halla dividiendo la frecuencia absoluta entre el número de datos ,el total siempre será igual a 1,la frecuencia porcentual la hallamos aplicando una fórmula y su total será 100 o un valor muy aproximado
% = FR x 100 fórmula
finalmente hacemos un gráfico estadístico llamado
diagrama de barras , donde colocaremos los datos de la tabla Observa el ejemplo:
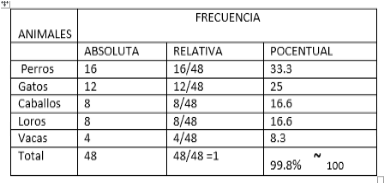
En una granja
encontré los siguientes animales; 16 perros, 12 gatos, 4 vacas, 8 caballos y 8
loros.
1. Hacemos una tabla de datos así:
2. Hallamos la frecuencia relativa. Para los
perros seria 16/48 y así sucesivamente
para cada dato
3. Hallamos el
porcentaje de cada dato y lo colocamos en la tabla de datos inicial. Observe
que para hallar el porcentaje utilizamos la frecuencia relativa.
% = FR x 100
La fórmula anterior la aplicamos
a cada uno de los datos y buscamos en la tabla la frecuencia relativa
Luego realizamos las operaciones indicadas. Para multiplicar por 100, solo agregue dos ceros al número
4. Trazamos un cuadrante del plano cartesiano ( eje X y eje Y) En el eje Y colocamos frecuencia absoluta , por lo tanto debemos dividir este eje de acuerdo con los datos de la tabla .
En el eje X colocamos los datos (animales) y levantamos rectángulos, desde el nombre del dato hasta la Fi , del mismo ancho y con la misma distancia
ACTIVIDAD A DESARROLLAR #1

4.
Convierte las
siguientes expresiones decimales a fracciones comunes que tenga como denominador
una potencia de 10.
a) 0,6
b) 0,32
c) 0,7689
d) 3,7
5
a) 5. Pasar a número decimal las siguientes fracciones decimales
a) a, 234/10000 b. 4/10 c. 34/10 d. 56324/10000 e.12/10
d)
ACTIVIDAD A DESARROLLAR #2
La siguiente tabla muestra el número de muertos por el COVID
19 en algunos países del mundo (es solo un ejemplo):
a. COMPLETE
LA TABLA ANTERIOR, MOSTRANDO LOS PROCEDIMIENTOS
b. Realice un gráfico o diagrama de barras,
recuerde bien trazado y coloreadas las barras
c. ¿Cuál es el número de muertos entre
España y Méjico? Explique
e. ¿Cuánto le faltaría a Colombia para igualar los muertos de España y
Estados Unidos? Explique
NOTA:Como es guía virtual., en el asunto escribir nombre y grupo, enviar un solo ARCHIVO con todas las actividades. No hacer trabajos en word
Para el grupo 7.5 ctaborda@hernanvillabaena.edu.co
Recuerde en cada actividad se le pide todo el procedimiento, las respuestas solas , tendrán la mitad de la nota
Serán 2 notas: una para matemáticas y otra para estadística
Manejar
pares ordenados en el plano cartesiano
¿PARA QUE TE SIRVE LO QUE VAS A APRENDER?
Los números enteros tienen
aplicaciones tanto en situaciones de la vida cotidiana como en situaciones de
las ciencias. Por ejemplo, para conocer la variación de la temperatura,
para conocer ganancias o pérdidas; Es
tradicional asociar las ganancias de una transacción con números enteros
positivos, las pérdidas con enteros negativos y el 0 con aquellas transacciones
en donde no hay ni pérdidas ni ganancias. Para
el crecimiento o la disminución de la cantidad de agua en el río en diferentes
épocas del año, conocer acontecimientos
antes y después de un nacimiento por ejemplo, o simplemente saber la altura o
la profundidad respecto al nivel del mar.
El numero 0 pertenece al conjunto de
los números enteros es el único que no se considera negativo o positivo.
Un edificio tiene un ascensor que sirve para llevar a las personas hasta uno de sus cinco pisos, a una planta baja o a uno de sus tres sótanos.
El conjunto de todos los números enteros se representa :
En la recta numérica los números
negativos se encuentran a la izquierda del cero y los positivos a su derecha.
Si miramos el plano cartesiano, esta premisa también se cumple, pero adicional están
los números por encima del cero, que son positivos y por debajo del cero son
negativos
Números Opuestos
Al observar la recta numérica de los números enteros se puede determinar que existen parejas de números que se encuentran a la misma distancia de cero, aunque tengan signos diferentes ejemplo 7 y -7 se encuentran a 7 unidades del cero a pesar de tener signos distintos.
Dados dos números enteros cualesquiera representados en una recta numérica:
a) Es mayor el que está a la derecha.
b) Es menor el que está a la izquierda.
c) Son iguales si les corresponde el mismo punto.
Valor
absoluto de un número entero.
Los
números +3 y -3 se encuentran a la misma distancia del cero. Ocurre así porque
los dos números enteros están formados por el mismo natural, el 3, aunque con
distinto signo.
El número
natural 3 se llama valor absoluto de +3 y -3, y si indica así:
|+3| = |-3| = 3
Los números enteros pueden sumarse, restarse, multiplicarse y dividirse,
siguiendo el modelo de los números naturales añadiendo unas normas para el uso
del signo.
SUMA O ADICIÓN DE NÚMEROS ENTEROS
Para sumar dos
números enteros, se determina el signo y el valor absoluto del resultado del
siguiente modo:
·
Si ambos sumandos tienen el mismo
signo: ese es también el signo del resultado, y su valor absoluto es la suma de
los valores absolutos de los sumandos.
·
Si ambos sumandos tienen distinto
signo:
o El
signo del resultado es el signo del sumando con mayor valor absoluto.
o El
valor absoluto del resultado es la diferencia entre el mayor valor absoluto y
el menor valor absoluto, de entre los dos sumandos.
EJEMPLOS:
(+21) +
(−13) = +8
(+17) +
(+26) = +43
(−41) + (+19) = −22
(−33) +
(−28) = −61
RESTA O DIFERENCIA DE NÚMEROS ENTEROS
La resta de
dos números enteros (minuendo menos sustraendo) se
realiza sumando el minuendo más el sustraendo cambiado de signo.( suma el minuendo con el opuesto del
sustraendo)
MULTIPLICACION DE NUMEROS ENTEROS
En la multiplicación
de dos números enteros se determinan el valor absoluto y el signo del resultado
de la siguiente manera:
·
El valor absoluto es el producto de los valores absolutos de los
factores
·
El signo es «+» si los signos de los factores son iguales, y «−» si son
distintos.

EJEMPLOS:
(+5) × (+3) =
+15
(+4) × (-6) = -24
(−7) × (+8) = −56
(−9) × (−2) =
+18.
DIVISION DE NUMEROS ENTEROS
En la división de
dos números enteros se determinan el valor absoluto y el signo del resultado de
la siguiente manera:
·
El valor absoluto es el cociente de los valores absolutos del dividendo
y divisor.
·
El signo es «+» si los signos del dividendo y divisor son iguales, y «−»
si son distintos.
EJEMPLO:
(+15) : (+3) = +5
(+12) : (-6) = -2
(−16) : (+4) = −4
(−18) : (−2) = +9.
Observe el siguiente video que le puede ayudar con los signos , en las diferentes operaciones entre números enteros
https://www.youtube.com/watch?v=jpbceHN35xo
POTENCIACIÓN DE NÚMEROS ENTEROS
La potenciación se define como la operación que simplifica la multiplicación
de varios factores iguales, se multiplica el valor absoluto de la base por
sí mismo, tantas veces como indique el exponente y para determinar
el signo de la potencia se deben de tener en cuenta las siguientes reglas:
a)
Si la base es negativa y el exponente es par, la potencia es positiva
EJEMPLO: ( - 3 )2 = ( -3) (-3) = 9 o
(-3)2 = 9
b)
Si la base es negativa y el exponente impar, la potencia es negativa
EJEMPLO
: ( - 3)3
= - 27
c)
Si la base es positiva y el exponente es par o impar, la potencia es
positiva
EJEMPLOS: 24 = 16 y 23 = 8
RADICACION DE NUMEROS ENTEROS
La radicación es una operación inversa a la potenciación en la que, dadas
la potencia y el exponente, se debe hallar la base.
1. Observar que las raíces cuadradas de los números positivos tienen dos soluciones:
La positiva y la negativa:
2.- Las raíces cuadradas de los números negativos no tienen solución. o,
más exactamente, no tienen solución en
el campo numérico de los enteros.
ACTIVIDAD A DESARROLLAR #1
1 Realizar las siguientes operaciones con números
enteros:
a. (+5) x (+3) = b. (-7) x (+8) = c. - 56 : 8 =
d. –
18 : - 3 = e. (+8) : (-4)=
g. (-7) + 5 = h. (+10) – (+6) = i. (-15) – (-5) =
j. (- 4)2 = k. (-10)5 = l. (79)0 =
m. (-1)9 = n. 513 . 517 = o. (2/5)3 x (2/5)2 =
2. Ubicar los números de las siguientes operaciones en la recta numérica y dar su resultado:
a. 6 + (-3) = b. (-8) + 5 = c. (-2) +(-3) = d. 12+ (-9) =
PLANO CARTESIANO:
Plano cartesiano: está formado por dos rectas numéricas perpendiculares,
una horizontal y otra vertical que se cortan en un punto.
La recta horizontal es llamada eje de las abscisas o de las equis (x),
y la vertical, eje de las ordenadas o de las yes, (y); el punto donde
se cortan recibe el nombre de origen.
El plano cartesiano tiene como finalidad describir la posición de puntos,
los cuales se representan por sus coordenadas o pares ordenados.
Las coordenadas se forman asociando un valor del eje de las equis
a uno de las yes, respectivamente, esto indica que un punto (P)
se puede ubicar en el plano cartesiano tomando como base sus
coordenadas, lo cual
se representa como:
P (x, y)
Para localizar puntos en el plano cartesiano se debe llevar a cabo el
siguiente procedimiento:
1. Para localizar la abscisa o valor de x, se cuentan las unidades
correspondientes hacia la derecha si son positivas o
hacia la izquierda si son negativas,
a partir del punto de origen, en este caso el cero.
2. Desde donde se localiza el valor de x, se cuentan las unidades
correspondientes (en el eje de las ordenadas) hacia arriba si son positivas
o hacia abajo, si son negativas y de esta forma se localiza cualquier punto
dadas ambas coordenadas
De modo inverso, este procedimiento también se emplea cuando se requiere
determinar las coordenadas de cualquier punto que
esté en el plano cartesiano
En el punto A: del origen corrimos 5 lugares a la izquierda sobre el eje “X”
porque el número (-5) es negativo y 3 lugares hacia arriba sobre el eje “Y”
porque el número (3) es positivo, luego interpolamos las dos líneas
hasta que se unan y el punto donde se unen corresponde al par
ordenado (-5,3). Observe que el primer número del par ordenado
corresponde al
valor de las equis y el segundo a las yes
Ejemplo : ubicar en el plano cartesiano los pares ordenados
(3,4) y (-4 , -3)
1. Trazar el plano cartesiano, señalar el origen
2. Numerar los ejes ( derecha y arriba positivos, izquierda y abajo negativos
3. ubicar los 2 pares ordenados , según los signos del cuadrante
4. Unir los puntos resultantes
ACTIVIDAD A
DESARROLLAR #2
1. Para cada grupo de pares ordenados( a y b), trazar un plano
cartesiano para cada uno y ubicarlos, señalando el punto que
corresponda a cada par ordenado ( ver
ejemplo)
a) A:
(2,3) B: (-2,2)
C: (-3 , -1) D: (2,
-2) E: (4,0) F: (0,-5)
b) A: (2,4)
B: (4, -3) C: (0,4) D (-1 ,-1)
2. Ubicar en el plano cartesiano los siguientes pares ordenados y
al final unir los puntos
resultantes, para formar un figura geométrica
POLÍGONOS
REGULARES
Recuerde que un polígono regular es aquel que tiene todos sus
lados y ángulos internos iguales
PARTES DE UN POLÍGONO:
LADOS: son los segmentos que forman la linea poligonal
VÉRTICES:son los puntos donde se unen los lados
ANGULOS: son las regiones del plano que delimitan dos lados
DIAGONAL: Es la recta que une dos vértices no consecutivos
CENTRO: es el punto desde el cual todos los ángulos y lados están a la misma distancia
RADIO: es el segmento que une el centro del polígono con cualquiera de sus vértices
APOTEMA: es el segmento que une el centro del polígono con el centro de cualquiera de los lados
BASE: es el lado inferior de un polígono, normalmente es el lado en que se apoya la figura
Clasificación de
polígonos según sus lados:
- Triángulo: 3 lados
- Cuadrilátero: 4 lados
- Pentágono: 5 lados
- Hexágono: 6 lados
- Heptágono: 7 lados
- Octógono: 8 lados
- Eneágono: 9 lados
- Decágono: 10 lados
- Endecágono: 11 lados
- Dodecágono: 12 lados
EJEMPLO.
VÉRTICES:
A,B,C,D LADOS: AB, BC, CD, DA ÁNGULOS: DAB, ABC, BCD, CDA
DIAGONALES: AC,
BD
ACTIVIDAD A
DESARROLLAR #3
Trazar en tu cuaderno los 6 primeros polígonos que aparecen en la clasificación y a cada uno colocarle las partes: con letras mayúsculas indicas los vértices, las diagonales debes trazarlas todas, medir los ángulos internos de cada polígono regular y dar su valor total, o sea la suma de todos los ángulos internos
Enviar al correo ctaborda@hernanvillabaena.edu.co
Recuerde el orden de envío de las actividades y la puntualidad en la entrega
Cada actividad tiene una nota, asimismo la organización y puntualidad en la entrega
GUIA #2
MAYO 31 DE 2021
JERARQUIZACIÓN DE OPERACIONES Y USO DE SIGNOS DE
AGRUPACIÓN
OBJETIVO:
Razonar y realizar
operaciones entre los enteros aplicando la jerarquía de operaciones y los
signos de agrupación
Construir cuerpos sólidos y
reconocer su elementos básicos
Obtener información arrojada
por un diagrama circular
La jerarquía de operadores determina el
orden en el que se resuelven las expresiones cuando se involucran operaciones aritméticas
como la suma, resta, multiplicación, división, potencia y raíz.
Ejemplo:
Para
resolver 3 x 6 + 4.
Podría
interpretarse como: 3 x (6 + 4) = 3 x 10 = 30.
O bien,
como: (3 x 6) + 4 = 18 + 4 = 22.
De igual
manera, 8 x 3 + 5 se podría interpretar como:
8 x (3 +
5) = 8 x 8 = 64 o también como (8 x 3)
+ 5 = 24 + 5 = 29.
¿Cuáles
serían los resultados correctos?
Para
evitar confusiones y errores se ha convenido en que cuando no hay paréntesis,
dado que los signos + y – separan cantidades, se efectúan las operaciones en el
siguiente orden de izquierda a derecha.
- Potencias y raíces
- Multiplicaciones
y Divisiones
- Adiciones
y Sustracciones
Por
tanto, retomando los ejemplos del principio:
3 x 6 + 4
= 18 + 4 = 22
8 x 3 + 5
= 24 + 5 = 29
Observemos otros ejemplos:
6 x 22
+ 3 = 6 x 4 + 3 = 24 + 3 = 27
En este
caso, siguiendo el orden, se comienza por resolver las potencias (22),
después la multiplicación y finalmente la suma o resta si hay.
+ 42 x 2 — 32 x 4 =
Primero
se resuelven las potencias: 42 = 16 y 32 = 9
La operación
queda así: 5 + 16 x 2 — 9 x 4 =
Después
se resuelven las multiplicaciones: 16 x 2 = 32 y 9 x 4 = 36
5 + 32 —
36 =
El
siguiente paso es resolver la suma: 5 + 32 = 37
Y
finalmente la resta: 37 — 36 = 1
USO DE SIGNOS DE AGRUPACIÓN
En ocasiones se requiere usar paréntesis para
indicar que algunas operaciones se deben efectuar antes que otras, o bien, que
deben considerarse como un solo número. Los paréntesis como los corchetes [ ] y
las llaves { }, se utilizan para situaciones en las que intervienen varias
operaciones secuenciadas. Cuando un
polinomio aritmético tiene signos de agrupación, se elimina cada signo de
agrupación de adentro hacia a fuera, teniendo en cuenta el orden de las
operaciones y la ley de signos .Ejemplos:
1. Para
sumar (3 + 9) –4, se debe efectuar primero (3 + 9) y después restar 4 al
resultado.
(3 + 9) —
4 = 12 — 4 = 8
2. Para
sumar 3 + (9 – 4), se efectúa primero (9 - 4) y al sumando 3 se le añade el
resultado del paréntesis.
3 + (9 —
4) = 3 + 5 = 8
3. Resolver
: 6 + (4 + 23)
Primero
se resuelve la potencia: 2 x 2 x 2 = 8
Después
se realiza la suma que está entre paréntesis: (4 + 8 = 12)
Finalmente
se resuelve la operación completa: 6 + 12 = 18
SIGNOS DE UN
Un
paréntesis precedido del signo + puede eliminarse sin afectar el signo de los
sumandos que contiene.
Si el
signo que precede al paréntesis es negativo esto afecta al resultado de la
operación contenida en dicho paréntesis. Ejemplos:
Ejemplo:
+ (7 — 2)
+ 3 = 5 + 3 = 8 = (7 — 2) + 3 = 5 + 3 =
8
- 5 - (32 —
23)
En este
ejemplo, primero se resuelven las potencias que se ubican dentro del
paréntesis:
3 x 3 = 9
2 x 2
x 2 = 8
De esta
manera se resuelve la resta del paréntesis: 9 — 8 = 1
Posteriormente se realiza la operación completa: --5 — 1 = - 6
ACTIVIDAD A DESARROLLAR #1
Aplica La jerarquía de
operaciones y el uso de los signos de agrupación. Recuerda realizar el proceso ( vale 1 nota)
a) 52 –7 + 3 – 14 =
b) 6.4 + 5 + 7 – 3 =
c) 33 +( 6 + 2) + 8 =
d) 9 – 3 + 8 / 4 =
e) 9 − 7 + 5 + 2 − 6 + 8 − 4 =
f) 10 / 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 2 − 16 / 4 =
g) 23 + 10 / 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 22 − 18 / 3 =
h) 6 - [5 + 4 - (7 – 3) ] =
i) [(7 + 5) + 3] + [(7 – 1) + 2 ] =
j) (5 – 7) + (8 + 9 ) – 11 =
k) [(8 + 2) / 5] + [(6 – 3) ÷ 3] =
l) 3 +7 – [ 5 + (8 ÷ 2 ) ] =
DIAGRAMA CIRCULAR
El diagrama circular (también llamado gráfica circular, gráfica de pastel o diagrama de sectores)
sirve para representar variables cualitativas o discretas. Se utiliza para representar la
proporción de elementos de cada uno de los valores de la variable.
Observa el siguiente
ejemplo:
Se realiza una encuesta
para escoger el color representativo de un equipo y los resultados
fueron:
Rosa 7 personas, amarillo
11 personas, azul 5 personas, verde 15 personas, y rojo 2 personas
Con estos datos
construimos la tabla de frecuencia ( 4 columnas)
Luego de tener la tabla completa, trazamos una circunferencia y su radio y a continuación con la ayuda del transportador medimos el primer ángulo de la tabla
Apoyando el transportador en la última línea trazada
siempre, medir el segundo ángulo y así
sucesivamente hasta terminar
Título del diagrama (
según lo que plantee el problema)
Cada porción
correspondiente a un ángulo se colorea de forma diferente
Se pueden colocar internamente los
valores de los ángulos hallados y MEDIDOS
Hacer un cuadro de
convenciones que contenga : los colores, el valor del Angulo y el porcentaje,
es muy importante para hacer los análisis estadísticos que se pidan
Ejemplo :
¿Por qué en el diagrama
el color verde ocupa más espacio?
El mayor número de
personas, votaron por el color verde: Frecuencia =15
El valor del ángulo fue
de 135°
El porcentaje de personas
que votaron en la encuesta por el color verde fue del 37.5%
Muy superior a los demás
datos de la encuesta
Observe el siguiente video para que su trabajo sea mas productivo
ACTIVIDAD A DESARROLLAR #2
Para celebrar el final del año en una empresa, se desea saber cuál es el refrigerio deseado por los trabajadores y el supervisor hace un sondeo sobre sus preferencias. Estos fueron los resultados: 15 trabajadores prefieren hamburguesas, 20 salchipapas, 15 pizza y 10 arroz con leche
De acuerdo con la información anterior:
1. Construir una tabla de frecuencia, colocar los
datos y la frecuencia
2. Hacer todas las operaciones para hallar el
porcentaje de cada comida ( resultado a la tabla)
3. Hacer todas las operaciones para hallar el valor
del ángulo ( resultado a la tabla
4. Trazar una circunferencia y su radio, a partir
de él medir y trazar cada uno de los ángulos , pintar cada ángulo de un color
diferente
5. Colocar el título al gráfico y hacer tabla de
convenciones como en el ejemplo
Leer en el diagrama
la información recogida y RESPONDER:
A. ¿Qué significa el mayor ángulo encontrado en tu
diagrama?
B. ¿Cuánto suman los % encontrados para el arroz con leche y la
pizza?
C. ¿Cuánto le falta al % del arroz con leche para
igualar el % de las salchipapas?
VALE UNA NOTA
CUERPOS
Los cuerpos geométricos son figuras tridimensionales con anchura, altura y profundidad tales como los poliedros, prismas, icosaedros, esferas,…
Los cuerpos geométricos son las figuras geométricas de tres dimensiones.
POLIEDROS
Un poliedro es la región del espacio delimitada por
polígonos, o lo que es lo mismo, un cuerpo geométrico cuyas caras son planas
que encierran un volumen finito.
Los elementos notables de un poliedro son los
siguientes:
·
Caras: Cada uno de los polígonos que limitan el poliedro
·
Aristas: Los lados de las caras del poliedro. Dos caras tienen una
arista en común.
·
Vértices: Los vértices de cada una de las caras del poliedro. Tres caras
coinciden en un mismo vértice.
·
Ángulos diedros: Ángulos formados por cada dos caras que tienen una
arista en común.
·
Ángulos poliédricos: Los ángulos formados por tres o más caras del
poliedro con un vértice común.
·
Diagonales: Segmentos que unen dos vértices no pertenecientes a la misma
cara.
PARA MAYOR COMPRENSIÓN DE LOS ÁNGULOS DIEDROS Y POLIEDROS OBSERVE:
Ángulo diedro: Es la proporción de espacio limitada por dos semiplanos que se llaman cara
Ángulo poliedro: Es la proporción de espacio limitada por tres o más planos que concurren en un punto llamado vértice. Un ángulo poliedro debe medir menos de 360°
ACTIVIDAD A DESARROLLAR #1.
Observe las siguientes figuras:
Trazarlas en su cuaderno y señalar los siguientes
elementos en cada una de ellas
. Caras
.vértices . Aristas. un ángulo
diedro y un ángulo poliedro
Colorear las caras
2. Armar el cuerpo y enviar un corto video realizando
el trabajo de armado
Los estudiantes de guía física, realizan los dibujos
de los cuerpos armados
En google pueden
buscar plantillas para tetraedro y cubo de mayor tamaño
Valor: 2 notas
Una nota por los elementos señalados en el cuaderno
y otra nota por los cuerpos sólidos armados
BIBLIOGRAFIA.
https://www.sangakoo.com/es/temas/poliedros-figuras-basicas-y-clasificacion
https://www.universoformulas.com/matematicas/geometria/cuerpos-geometricos/
CONSUELO TABORDA Whatsapp 3128364393
Correo electrónico ctaborda@hernanvillabaena.edu.co
Recuerde: no presentar trabajos en word
FECHA DE ENTREGA JUNIO 7/2021
DESPUÉS DE ESTA FECHA SERÁN CALIFICADOS SOBRE 3.0
|
|



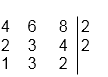














































No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.