POTENCIACIÓN DE NÚMEROS NATURALES
OBJETIVO: Repasar y afianzar los conocimientos sobre multiplicación de números naturales.
La potenciación es
la operación que nos permite hallar el producto de factores iguales.
ELEMENTOS:
BASE: es el factor que se
repite
EXPONENTE: es el número que
indica cuantas veces se repite la base
POTENCIA: es el resultado de
multiplicar la base, tantas veces indique el exponente
Según los
elementos nombrados, de éste ejemplo podemos decir.
El factor 2 que
se repite se llama base y el 5 que es el exponente indica que la
base se repite 5 veces, para obtener el número 32 que es la potencia
Las siguientes multiplicaciones:
1.
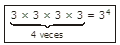
todos los factores de ésta multiplicación son iguales y el factor se repite cuatro veces.Por lo tanto:
entonces: 34 = 81 --------Potencia
2.
entonces: 43 = 64
Multiplicamos tres veces el número cuatro para hallar la potencia (64)
De lo anterior
podemos concluir que: “Una
potencia es el producto de números iguales”
Observa 23 = 6 y
23 = 8 ¿Cuál es la potencia correcta?
23 =
6 es falsa. No
se multiplica la base por el exponte
23 =
8 es correcta. multiplicamos tres veces el numero dos
(2x2x2)
Cuando nos dan el
producto:
|
Producto |
Base |
Exponente |
Potencia |
|
6 x 6 x 6 |
6 |
3 |
216 |
# que se repite las veces que se repite producto de factores
Cuando nos dan la potencia:
54
|
Potencia |
Base |
Exponente |
Desarrollo |
Valor de la potencia |
|
54 |
5 |
4 |
5 x 5 x 5 x 5 |
625 |
Observa el siguiente video con atención, puedes encontrar conceptos valiosos
https://www.youtube.com/watch?v=JhXkQulf9MM
LECTURA DE POTENCIAS
Cada potencia se puede leer de dos formas diferentes. Observa estos ejemplos:
PROPIEDADES DE LA POTENCIACIÓN
1. PRODUCTO DE POTENCIAS DE IGUAL BASE:
El producto de potencias con la misma base, será igual a
la misma base, elevada a la suma de los exponentes
Ejemplo: 63 . 62 =
6 3+2 ---------- 63
. 62 = 65
2. POTENCIAS
DE EXPONENTE 1
La potencia de exponente 1 de un número es igual a
dicho número.
Ejemplos : 61 = 6 y 81
= 8
3. POTENCIAS
DE EXPONENTE 0
La potencia de exponente 0 de un número es igual a
1.
Ejemplos :
50 = 1 -
70 = 1 -
120 = 1
ACTIVIDAD A DESARROLLAR #1
COMPLETE LAS SIGUIENTES TABLAS
|
Producto |
Base |
Exponente |
Potencia |
|
2X2X2X2X2X2 |
|
|
|
|
4X4X4X4 |
|
|
|
|
8X8X8x8 |
|
|
|
|
12X12X12 |
|
|
|
|
7X7X7X7X7 |
|
|
|
|
9X9X9X9X9X9 |
|
|
|
|
|
|
|
|
|
Potencia |
Base |
Exponente |
Desarrollo |
Valor |
|
35 |
3 |
5 |
3x3x3x3x3 |
243 |
|
27 |
|
|
|
|
|
104 |
|
|
|
|
|
63 |
|
|
|
|
|
44 |
|
|
|
|
|
56 |
|
|
|
|
|
NOMBRE |
POTENCIA |
|
Cinco elevado a la cuarta |
|
|
Siete elevado al cubo |
|
|
Ocho elevado a la quinta |
|
|
Doce elevado al cuadrado |
|
|
Dos elevado a la octava |
|
|
Cuatro elevado a la sexta |
|
|
Diez elevado a la séptima |
|
|
Potencia |
Nombre |
|
36 |
|
|
104 |
|
|
76 |
|
|
98 |
|
|
253 |
|
|
86 |
|
|
56 |
|
ACTIVIDAD A DESARROLLAR #2
Escriba el valor de cada potencia.
a. 112 =
d. 64 = g. 27 =
j. 124 =
b. 152 =
e. 83 =
h. 94 =
k. 133 =
c. 172 =
f. 105 =
i. 203 =
l. 79 =
ACTIVIDAD A DESARROLLAR # 3
Según las propiedades de la potenciación exprese
los resultados para:
a. 33 . 32 . 34 = b.
71 . 74 = c. 125 . 122 = d. 151 = e.
80 =
f. 101
= g. Como resolverías 42 + 41 = ?
Para los grupos
6º1, 6º2, 6º3 y 6º4 enviar a: yamiberrio@hernanvillabaena.edu.co
Para el grupo 6.5 enviar a: ctaborda@hernanvillabaena.edu.co
Para la guia virtual tener en cuenta: en el asunto escribir nombre del estudiante y grupo y enviar un solo correo con
todas las actividades.
RADICACIÓN
La radicación es la
operación inversa a la potenciación. Y consiste en que, dados dos números,
llamados radicando e índice, hallar un tercero, llamado raíz,
tal que, elevado al índice, sea igual al radicando.
Observe el siguiente ejemplo:
Hallar la raíz :
Tenemos que el radicando es 81 y que el índice es 2
Para hallar la raíz debes
preguntarte: cuál es el número que multiplicado por sí mismo 2 veces me da 81
Tienes 9x9 = 81 esto es lo mismo
que tener 92 =81
Por lo tanto el número que multiplicamos por sí mismo es la raíz:
En la raíz cuadrada el índice es 2,
aunque generalmente se omite. Consistiría en hallar un número conociendo su
cuadrado.
El procedimiento es el mismo que en el ejemplo anterior
El número que multiplicado por sí mismo 2 veces es:
6x6 = 36 o 62 = 36 quiere decir que la Raíz es 6
La raíz cuadrada de un número a, es exacta cuando encontramos un número x, que elevado al cuadrado (n) es igual al radicando: x2 = a.
Raíz cuadrada
exacta
La raíz cuadrada exacta tiene de resto 0.
Son los números que poseen raíces cuadradas
exactas.
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144,
169, ...
En el caso de otras raíces se procede de igual
manera
Ejemplo
Cual será el número (x) que multiplicado por sí mismo veces(n), me da el radicando (a)
3x3x3= 33 y 33 = 27
Observa el siguiente video para que hagas un repaso de potenciacion y radicacion
LA
LOGARITMACIÓN
Observamos
una serie de elementos, como:
a) La
base: Es el número que elevado al exponente nos da el número total. a
b) El
número total: Es el resultado n
c) El logaritmo: Es el exponente al cual debemos elevar la base para obtener el
total. x
La potenciación, la radicación y la logaritmación son operaciones equivalentes pero escritas de forma diferente
ACTIVIDAD A DESARROLLAR # 1
1. CALCULAR LAS SIGUIENTES RAÍCES Y JUSTIFICAR LA RESPUESTA, ayúdate del Ejemplo
2. COMPLETAR EL SIGUIENTE CUADRO
Hasta la actualidad se han
desarrollado muchas y muy variadas técnicas estadísticas que se aplican en
laboratorios y todo tipo de organizaciones alrededor del mundo en todos o casi
todos los campos del conocimiento humano, lo que hace de la Estadística en sí
misma una ciencia muy importante en el desarrollo de la vida.
LOS ELEMENTOS DE LA ESTADÍSTICA
Los ELEMENTOS la estadística que vamos a usar a partir de
ahora son: población, muestra y variable.
- La Población: es el universo de los elementos estudiados, es el conjunto de todos los posibles
elementos que intervienen en un experimento o en un estudio.
- la muestra es una parte de la población sobre la que se hace el
estudio estadístico
- la variable es la pregunta o aquello que se está investigando, en nuestro caso solo estudiamos dos tipos de variable cualitativas (representadas por una cualidad) y cuantitativas (representadas por un numero
Ejemplo: En el supermercado “Las Margaritas “se realiza una encuesta a 50 personas sobre la marca de arroz preferida.
- Población: todas las personas que van al supermercado.
- Muestra: 50 personas del supermercado
- Variable: marca de arroz (cualitativa)
- Población: todas las personas que van al supermercado.
ACTIVIDAD A DESARROLLAR # 2
Determinar población, muestra, variable y tipo de variable en las siguientes situaciones.
- En la unidad residencial “El Paraíso” se pregunta a 80 familias por el número de personas que conforman el grupo familiar.
- Se pregunta a 150 jóvenes en edades entre 13 y 15 años del barrio “el
Canelo” sobre su deporte favorito.
- Se realiza una encuesta a los empleados del hospital “Santa Ana” sobre
la enfermedad más común, para ello, se pregunta a 20 doctores del servicio
de urgencias.
Al enviar su trabajo no olvide en el asunto
escribir nombre completo y grupo
fotos en forma vertical
Para el grupo 6°5 ctaborda@hernanvillabaena.edu.co
FECHA DE ENTREGA: la fecha máxima para entregar su guía es el lunes 9 de Marzo hasta el mediodía
·
Comprende y demuestra la equivalencia entre fracciones
· Sustenta de forma correcta la transformación de fracciones en número mixto
. Representa diferentes triángulos y su clasificación
En matemáticas una fracción, número fraccionario, es la
expresión de una cantidad dividida entre otra cantidad; es decir que
representa un cociente no efectuado de números.
Para
expresar los números fraccionarios, se necesitan dos números llamados numerador
y denominador. El número que expresa en cuántas partes iguales está dividida la
unidad y se escribe debajo de la raya horizontal, es el denominador; y el
número que indica o numera las partes que se toman es el numerador y se escribe
encima de la raya horizontal.
“El numerador indica el número de partes que se toman de la unidad y el denominador en cuantas partes iguales se divide esa unidad.”
En la figura vemos a fracción 2/6 , área sombreada .La unidad se dividió en 6 partes iguales y se tomaron 2
LECTURA DE UN NÚMERO
FRACCIONARIO
En un número fraccionario se lee primero el numerador y luego el denominador. Para leer el denominador hay que tener en cuenta que hasta diez los denominadores se leen de forma especial y que de 11 en adelante se lee el número y se agrega la terminación avos.
Si una unidad o una cosa la dividimos en 2, 3, 4, 5, etc. pedazos o fracciones iguales, cada parte es un medio, un tercio, un cuarto, un quinto, un sexto, un séptimo, un octavo, un noveno, un décimo, un onceavo, un doceavo, etc.
Ejemplos
se lee dos tercios
8/10 = ocho decimos
6/13 = seis treceavos
CLASIFICACIÓN DE FRACCIONES:
v Las fracciones propias son aquellas cuyo numerador es menor que el denominador, es decir, son menores que la unidad.
Ejemplo 5/ 8 ![]()
v Las fracciones impropias son aquellas cuyo numerador es igual o mayor que el denominador, es decir, son iguales o mayores que la unidad. Ejemplo 15/4
observe el video:
https://www.youtube.com/watch?v=pOykmkuRnw4&list=PLeySRPnY35dH5PTh8sRqEHkzxbez41Bex
NÚMEROS MIXTO
Los números mixtos son los formados por unidades enteras y unidades fraccionarias.
Los números mixtos se escriben poniendo primero el entero, y a continuación el fraccionario; y se leen enunciando el entero seguido del nombre de la unidad principal, y luego el fraccionario.
Ejemplo
TRES ENTEROS Y UN SEXTO
Transformación de fracciones impropias en números mixtos
Para transformar fracciones impropias en números mixtos se divide el numerador entre el denominador y el número mixto queda formado por el cociente como la parte entera y una fracción cuyo numerador es el residuo y cuyo denominador es el mismo de la fracción dada.
Ejemplo
Transformar 7/4 a número mixto:
Transformación de números mixtos en fracciones impropias
Para transformar un número mixto en fracción impropia, se multiplica el entero por el denominador dado, al producto se le suma el numerador, y se pone por denominador de la fracción dada.
https://www.youtube.com/watch?v=Zf4KEQfm1aY&t=228s
FRACCIONES
EQUIVALENTES
Dos fracciones son equivalentes si representan la misma cantidad o el mismo núm
Veamos un ejemplo.
Decir si las siguientes fracciones son
equivalentes.
Para verificar si dos fracciones son
equivalentes basta ubicar una fracción al lado derecho de la otra y chequear,
que el producto del numerador de la primera por el denominador de la segunda
sea igual al producto del denominador de la primera por el denominador de la
segunda.
Veamos un ejemplo.
Decir si las siguientes fracciones son
equivalentes.
Vemos que ambos productos son
iguales, por lo tanto podemos concluir que son equivalentes.
ACTIVIDADES A
DESARROLLAR : VALEN UNA NOTA
observe muy bien el video y mire que toma parejas de fracciones para saber si son equivalentes, mediante la multiplicación de extremos y medios

6. 6. Marcar si estas parejas de números fraccionarios son equivalentes o no. En caso afirmativo, deben escribir un signo igual (=), en caso negativo, si la fracción no es equivalente, dejar en blanco o marcar con una X.
RECUERDE: LAS ACTIVIDADES SE DEBEN ENVIAR CON LOS PROCESOS REQUERIDOS PARA SU SOLUCIÓN
Vi videos que te ayudaran en la equivalencia de fracciones
https://www.youtube.com/watch?v=DW0oILmN7c4
https://www.youtube.com/watch?v=PhuNOX9mavU
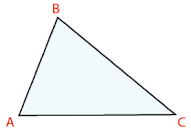
Figura geométrica formada por tres
segmentos de recta determinados por tres puntos no colineales.
ELEMENTOS DEL TRIANGULO:
VÉRTICES: A,B,C
LADOS: AB - BC- CA
ÁNGULOS: α - β- ϒ
PERÍMETRO: p
P= AB + BC +CA
CL CLASIFICACION DE TRIANGULOS
A. A. SEGÚN LA MEDIDA DE SUS LADOS
![]() El triángulo se designa por las tres
letras mayúsculas de sus vértices en cualquier orden, precedidos por el símbolo
El triángulo se designa por las tres
letras mayúsculas de sus vértices en cualquier orden, precedidos por el símbolo
N NOTA:
Para
los grupos 6º1, 6º2, 6º3 y 6º4 yamiberrio@hernanvillabaena.edu.co
Para el grupo
6.5 ctaborda@hernanvillabaena.edu.co
En el asunto escribir
nombre y grupo, no presentar trabajos en WORD
Si no están los
procedimientos , no se calificara solo la respuesta
SE EVALUARA LA PUNTUALIDAD Y ORDEN AL PRESENTAR LAS ACTIVIDADES
recuerde mandar las fotos en el mismo orden que están las actividades
GUIA #2
MAYO 31/2021
OPERACIONES CON NÚMEROS FRACCIONARIOS
· OBJETIVO
Realizar
diferentes operaciones sencillas con números fraccionarios
Interpretar datos representados en tablas y sacar conclusiones estadísticas.
FRACCIONES HOMOGÉNEAS: se llaman fracciones homogéneas a
aquellas que comparten el mismo denominador
FRACCIONES HETEROGÉNEAS: se dice que dos o más fracciones
son heterogéneas, cuando los denominadores son diferentes
OPERACIONES CON FRACCIONES
Observa : sumamos los numeradores ( 3+1 =4) y colocamos el mismo denominador, por eso el resultado es 4/8
¡Nunca sumamos los denominadores
En caso de
realizar sustracciones o RESTAS entre
fracciones homogéneas, procedemos de la misma manera que en la suma, pero en
este caso, estamos restando los numeradores
Ejemplo:
restamos los numeradores (7 - 3 =4) y colocamos el mismo denominador
MULTIPLICACION Y DIVISION PARA
FRACCIONES HOMOGENEAS Y HETEROGENEAS
En la MULTIPLICACIÓN lo que debemos hacer es multiplicar por un lado los numeradores y por otro lado los denominadores.
Ejemplo:
Los numeradores
se multiplican (5.1 = 5)
Los denominadores
se multiplican (7.7 = 49)
El resultado
será 5/49
En la
multiplicación podemos utilizar el signo tradicional (x) o simplemente un punto
entre los factores que también indica multiplicación.
El cociente o
sea la DIVISIÓN, es otra
fracción que resulta de multiplicar el numerador de la primera por el
denominador de la segunda ( este será el nuevo numerador) y el denominador de la primera por el numerador de la segunda (este será el
nuevo denominador) o viceversa
Dicho de otra
forma se multiplican en cruz las dos fracciones
El signo de la
división entre fracciones será : , o el signo tradicional de la
división
Ejemplo:
SUMA Y RESTA DE FRACCIONES
SUMA:
1. Buscamos un
denominador común para las fracciones, multiplicando entre si los denominadores
2.
Multiplicamos el numerador del primero por el denominador del segundo y el
denominador del primero por el numerador del segundo, separando estas
operaciones por signo +
4. Realizamos
la suma y damos el resultado
R/
RESTA:
En el caso de
la resta se procede de igual manera que en la suma , pero con el signo menos
entre los factores
Ejemplo :
entre los términos colocamos el signo menos (-) por ser una resta
NOTA: En caso
que sean más de dos fracciones las que se van a sumar, se hace el procedimiento
para las dos primeras y con el resultado obtenido se hace nuevamente el mismo
procedimiento con la tercera fracción y así sucesivamente hasta terminar con
las fracciones dadas.
ACTIVIDAD A DESARROLLAR # 1
2. Resuelva los problemas y
operaciones dadas a continuación
DIAGRAMA DE BARRAS (GRÁFICO DE BARRAS)
Un gráfico de barras o gráfico de
columnas, es una forma de representar gráficamente un conjunto de datos o
valores mediante barras rectangulares de longitud proporcional a los valores representados. Los gráficos
de barras pueden ser usados para comparar cantidades de una variable en
diferentes momentos.
TENGA EN CUENTA EN EL MOMENTO DE
REALIZAR EL GRÁFICO
·
El ancho
de la barra debe ser uniforme para todas las barras del diagrama.
·
La
longitud de la barra debe ser proporcional a la cantidad que representa.
·
El
espacio de separación entre barras por cada categoría debe ser constante.
·
Las
barras en estos gráficos pueden disponerse vertical u horizontalmente.
Es importante saber, que los datos
correspondientes a una variable los podemos colocar en una tabla de datos y que
luego miramos cuantas veces se repite cada dato, las veces que se repite un
dato se llama frecuencia ABSOLUTA,
la frecuencia RELATIVA se halla
dividiendo la frecuencia absoluta entre
el número de datos ,el total siempre será igual a 1.
La frecuencia porcentual la hallamos
aplicando una fórmula y su total será 100 o un valor muy aproximado
![]() % = FR x 100 formula
% = FR x 100 formula
finalmente hacemos un gráfico estadístico llamado
diagrama de barras , donde colocaremos los datos de la tabla Observa el ejemplo:
En una granja
encontré los siguientes animales; 16 perros, 12 gatos, 4 vacas, 8 caballos y 8
loros.
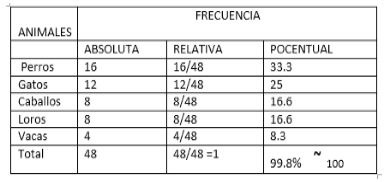
1. Hacemos una tabla de datos
2. Hallamos la
frecuencia relativa.( frecuencia absoluta/total de datos) Para los perros seria
16/48 y así sucesivamente para cada dato
3. Hallamos el
porcentaje de cada dato y lo colocamos en la tabla de datos inicial. Observe
que para hallar el porcentaje utilizamos la frecuencia relativa.
% = FR x 100
La fórmula anterior la aplicamos
a cada uno de los datos y buscamos en la tabla la frecuencia relativa
Luego realizamos las operaciones
indicadas. Para multiplicar por 100, solo agregue dos ceros al numero
![]()
![]()
4. Trazamos un cuadrante del plano cartesiano ( eje X y eje Y)
En el eje Y colocamos frecuencia absoluta , por lo tanto
![]() debemos dividir
debemos dividir ![]() este eje de acuerdo con los datos de
la
este eje de acuerdo con los datos de
la
![]()
![]() tabla. En el eje X colocamos los
datos (animales)
tabla. En el eje X colocamos los
datos (animales)
![]()
![]()
![]() Levantamos rectángulos, desde el nombre del dato
Levantamos rectángulos, desde el nombre del dato
Hasta la Fi , del mismo ancho y con la misma distancia
ACTIVIDAD A DESARROLLAR #2
La tabla presentada muestra el número de visitantes a
diferentes centros comerciales de la ciudad
|
CENTRO
COMERCIAL |
FRECUENCIA |
||
|
|
ABSOLUTA |
RELATIVA |
PORCENTUAL |
|
Unicentro |
30 |
|
|
|
Molinos
|
20 |
|
|
|
Oviedo
|
35 |
|
|
|
Santa
fe |
60 |
|
|
|
Florida
|
5 |
|
|
|
Total |
150 |
|
|
a. COMPLETE
LA TABLA DE FRECUENCIA Y MUESTRE LOS PROCEDIMIENTOS para hallar los %
b. Realice un gráfico o diagrama de barras,
recuerde bien trazado y coloreadas las barras
c. ¿Cuál es el número de visitantes entre Unicentro y Molinos? Explique
d. ¿Qué significa la barra más pequeña en el diagrama? Explique
e. ¿Cuánto le faltaría al centro comercial florida para igualar los
visitantes de Santa fe y Oviedo? Explique
f. ¿Qué porcentaje suman los visitantes de los 3 primeros centros
comerciales?
Para el grupo 6.5 ctaborda@hernanvillabaena.edu.co
En el asunto escribir
nombre y grupo, no presentar trabajos en WORD
Si no están los procedimientos ,
no se calificara solo la respuesta
FECHA DE ENTREGA: JUNIO 7 DE 2021
Trabajos entregados después de la fecha tendrán rebaja en la nota ( sobre 3.0)
![]()




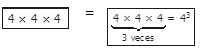




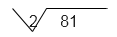















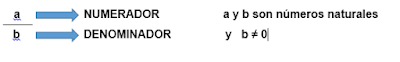




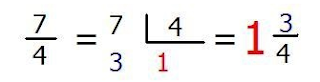



























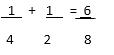



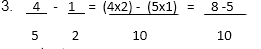







No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.